데이터분석 공부/통계 정리
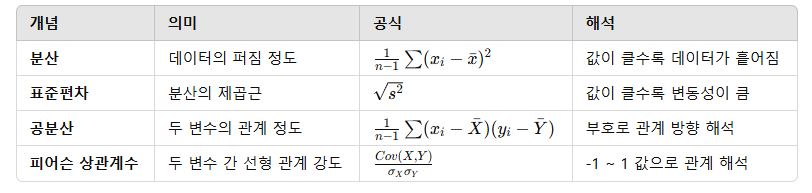
분산, 표준편차, 공분산, 피어슨 상관계수
sedin2
2025. 2. 25. 10:25
1. 분산

▶️ 개념
데이터가 평균을 중심으로 얼마나 퍼져 있는지를 나타내는 값이야.
쉽게 말해서, 데이터들이 평균 근처에 모여 있는지, 아니면 멀리 흩어져 있는지를 숫자로 나타낸 거야.
▶️ 표본과 모집단

▶️ 분산 구하는 공식

💡 왜 n−1을 쓰는 걸까?
표본을 사용해서 모집단을 추정하는 경우, 표본만으로 모집단의 분산을 완벽히 알기 어렵기 때문에 "불편 추정량"을 사용해서 n−1n-1로 나누는 거야.
2. 표준편차

▶️ 개념
분산은 "제곱"을 해서 원래 데이터와 단위가 달라지는데, 표준편차는 분산의 제곱근을 씌워 원래 데이터 단위로 변환한 값이야.
즉, 표준편차가 크면 데이터가 평균에서 많이 흩어져 있다는 뜻이야.
▶️ 표준편차 구하는 공식
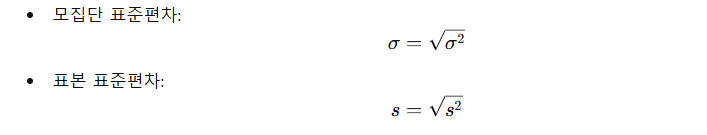
▶️ 예제

👉 표준편차가 10이므로, 학생들의 점수가 평균 80점에서 ±10 정도의 차이를 가진다고 볼 수 있어!
3. 공분산
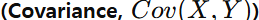
▶️ 개념
공분산은 두 변수가 함께 어떻게 변하는지를 나타내는 값이야.
- 양수 → 두 변수가 함께 증가하거나 감소하는 경향이 있음. (예: 키가 클수록 몸무게도 증가)
- 음수 → 한 변수가 증가하면 다른 변수는 감소하는 경향이 있음. (예: 운동 시간 증가 → 체중 감소)
- 0에 가까움 → 두 변수 사이에 관계가 거의 없음.
▶️ 공분산 구하는 공식

📌 문제점: 공분산은 값이 크면 관계가 강한 것 같아 보이지만, 데이터의 단위에 따라 값이 달라져 해석이 어려워.
그래서 상관계수를 사용해!
4. 피어슨 상관계수

▶️ 개념
피어슨 상관계수는 공분산을 표준화한 값으로, 두 변수 간의 "선형 관계" 강도를 -1에서 1 사이의 값으로 나타내.
▶️ 피어슨 상관계수 공식
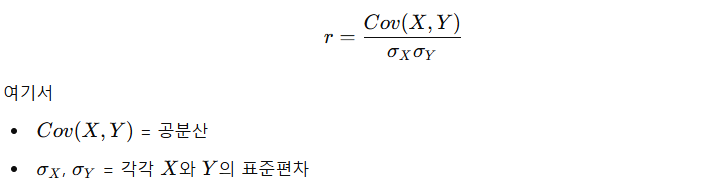
▶️ 해석
- r = 1 → 완벽한 양의 상관관계 (정비례, XX 증가 → YY 증가)
- r = − 1 → 완벽한 음의 상관관계 (반비례, XX 증가 → YY 감소)
- r = 0→ 상관관계 없음 (두 변수는 무관)
- r 값이 1 또는 -1에 가까울수록 선형 관계가 강함
▶️ 예제
💡 예를 들어, 학생들의 공부 시간과 시험 점수를 조사했더니
- 공부 시간이 많을수록 점수도 높아지는 경향이 있었다면 r 값은 0.8~1 사이
- 공부 시간과 점수 사이에 거의 관계가 없다면 r값은 0에 가까움
- 공부 시간이 많을수록 오히려 점수가 낮아진다면 값은 -0.8~-1 사이
📌 요약